Tiefe neuronale Netzwerke, sogenannte Deep-Learning-Netzwerke, sind die aktuellen Zugpferde der Künstlichen Intelligenz (KI). Ein neuronales Netzwerk ist ein tief verschachteltes System mit einem Schichtenkonzept von verschiedenen Neuronen, die miteinander verknüpft sind.
Das so entstandene tiefe Netzwerk, das einigen Konzepten im menschlichen Gehirn nachempfunden ist, ist keine einfache if-else-Maschine mehr, im Prinzip ist das trainierte Netzwerk eine Blackbox, die selbst der Erschaffer dieses Netzwerk nicht mehr selbst versteht.
Das Netzwerk besitzt einige sogenannte Hyperparameter, die es grundlegend konfigurieren. Beispiele dieser Hyperparameter sind die Anzahl der Schichten, die Anzahl von Neuronen pro Schicht, der Lernrate oder der Optimierungsalgorithmus. Die Auswahl dieser Parameter ist dem menschlichen Ersteller des Netzwerkes überlassen und gleicht eher einer Kunst als einer streng logischen Vorgehensweise. Oft muss durch einfaches Ausprobieren der verschiedenen Parameter das beste Netzwerk zusammengestellt werden, um damit das beste Ergebnis zu erzielen.
Einführung in neuronale Netzwerke – Beispiel mit DeepLearning4J
Als Startpunkt dient uns das einfache neuronale Netzwerk in Listing 1, welches den MNIST-Datensatz als Eingabe benutzt. MNIST ist ein klassisches einfaches Problem. Es geht um Handschrifterkennung mittels einem neuronalen Netzwerk.
MultiLayerConfiguration conf = new NeuralNetConfiguration.Builder()
.seed(rngSeed) //include a random seed for reproducibility
.activation(Activation.RELU)
.weightInit(WeightInit.XAVIER)
.updater(new Nesterovs(rate, 0.98))
.l2(rate * 0.005) // regularize learning model
.list()
.layer(0, new DenseLayer.Builder() //create the 1. input layer
.nIn(numRows * numColumns)
.nOut(500)
.build())
.layer(1, new DenseLayer.Builder() //create the 2. input layer
.nIn(500)
.nOut(100)
.build())
.layer(2, new OutputLayer.Builder(
LossFunction.NEGATIVELOGLIKELIHOOD)
.activation(Activation.SOFTMAX)
.nIn(100)
.nOut(outputNum)
.build())
.build();Das konfigurierte Netzwerk enthält einige Hyperparameter – zum Beispiel die Anzahl der Schichten, die Lernrate, Anzahl von Neuronen pro Schicht und die verwendeten Aktivierungsfunktionen. Unter [NeuralNets] findet der Leser eine gute Einführung in die grundlegenden Konzepte. In den sogenannten „Convolutional Neural Networks“, die eine Bilderkennung durchführen können, stecken noch mehr Hyperparameter wie „strides“ oder Filtergrößen. Es bleibt also viel Raum und Variabilität, ein Netzwerk zu schreiben, zu konfigurieren und zu optimieren.
Nachdem das konfigurierte Netzwerk wie in Listing 1 gezeigt trainiert wurde, ist es in der Lage, Handschriften zu erkennen (s. Abb. 1). Die Wahl der Hyperparameter ist nun der entscheidende Punkt im Netzwerk, die Anzahl der Schichten oder Neuronen ist zum Beispiel eine Entscheidung, die nicht offensichtlich ist; hier gibt es verschiedene Variationen, um ein gutes Netzwerk zu erstellen.

Abb. 1: Das Netzwerk kann Handschriften erkennen
Wie kann das Netzwerk optimiert werden?
Um nun ein Netzwerk sich selbst optimieren zu lassen, können verschiedene Methoden angewandt werden, einige befinden sich noch in der Erforschung, können aber schon aktiv mittels vorhandener Frameworks benutzt werden.
Die einfachste Methode, die verschiedenen Netzwerkparameter auszuprobieren, ist Brute Force. Diese Methode ist natürlich nicht sehr effizient, wenn man bedenkt, dass das Trainieren eines einzelnen Netzwerks mehrere Tage dauern kann und jede Änderung im Netzwerk dies erneut erfordert, um zu evaluieren, ob das neue Netzwerk besser abschneidet als das vorherige.
Ein aktueller Ansatz, der momentan von Google angetrieben wird, ist AutoML, das auf dem Verfahren „Neural Architecture Search“ beruht. Dieses wiederum nutzt das sogenannte „bestärkende Lernen“ (Reinforcment Learning, RL). Dieser Ansatz lernt anhand von Erfahrungen und verwendet sogenannte Belohnungen („rewards“), nachdem es eine Entscheidung getroffen hat. Je nach Belohnung (gut oder schlecht) kann es sich zur Laufzeit optimieren und dazulernen.
AutoML mittels Neural Architecture Search benutzt ein „policy gradient network“, um anhand der besten Belohnungen dem Idealziel näher zu kommen. Ein Controller, der selbst als „policy network“ implementiert ist, kann nun mittels der Belohnungen ein Kindnetzwerk aufbauen. Die Belohnungen aus dem Kindnetzwerk sind Validierungswerte, wie akkurat das Kindnetzwerk ist. Anhand dieser Belohnungswerte werden die Gewichte im Controller angepasst. Abbildung 2 zeigt das Konzept.
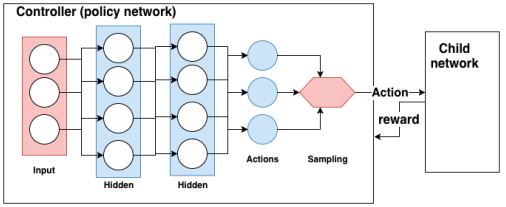
Abb. 2: Policy gradient Neural Architecture Search verdeutlicht das Konzept, welches auch aus AlphaGo bekannt ist.
AutoKeras [AutoKeras] ist ein weiteres Tool, um Neural Architecture Search umsetzen zu können. Es benutzt für das schrittweise Anpassen „Bayes’sche Optimierung“, da die Zielfunktion (unser Netzwerk) eine teure Zielfunktion ist. Eine interessante Anwendung zur Infrastrukturoptimierung mit Bayes’scher Optimierung bei Facebook findet sich unter [Bayesian].
Um nun unser simples neuronales Netzwerk in Listing 1 zu optimieren, stehen aktuell mehrere Techniken zur Verfügung, wie Bayes’scher Optimierung, Gradientenverfahren und genetische Algorithmen (s. Abb. 3). Jedes Verfahren hat seine Stärken und Schwächen bezüglich Aufwand und Performanz und alle werden erfolgreich für viele mögliche Optimierungsanforderungen benutzt. Der Artikel verwendet im Weiteren genetische Algorithmen, um unser Netzwerk zu optimieren.

Abb. 3: Techniken, um Neural Architecture Search umsetzen zu können
Optimierung und Selektierung durch Evolution
Der genetische Algorithmus ist einfach zu erklären, er basiert auf gezielter Selektion, Generationen, Populationen und Mutationen. Als Beispiel dient ein Netzwerk, das ca. 5 Minuten für das Training benötigt. Bei zum Beispiel vier möglichen Hyperparametern mit jeweils fünf verschiedenen Einstellungen würde es ca. (54) * 5 Minuten oder 52 Stunden dauern, um alle Parameter auszuprobieren – das ist zu lange!
Mit dem genetischen Algorithmus gibt es nun ein Konzept, um per Mutation und Selektion die beste Konfiguration auf evolutionäre Weise herauszufinden. Der genetische Algorithmus in Verbindung mit Deep-Learning-Netzwerken beinhaltet folgende Schritte:
- Es werden per Zufall „n“ Netzwerke erzeugt, um eine Population zu erhalten
- Jedes Netzwerk in der Population wird trainiert und danach wird eine sogenannte „fitness function“ angewendet, um zu evaluieren, wie gut jedes Netzwerk abschneidet. Im MNIST-Beispiel ist dies die „accuracy“ im Testdatensatz.
- Nachdem alle Netzwerke einen „score“ über die „fitness“-Funktion bekommen haben, werden diese nach den Besten sortiert und ein definierter Prozentsatz wird top-down in die nächste Generation übernommen.
- Es werden auch per Zufall einige Netzwerke in die nächste Generation übernommen, die nicht zu den „Top-Performern“ gehören – einige „Low-Performer“ bekommen somit auch eine Chance und die Gefahr, dass der Algorithmus in einem lokalen Maximum stecken bleibt, wird verringert
- Nachdem nun zum Beispiel in einer Population von 20 Netzwerken 8 übernommen und mutiert wurden (5 Top- und 3 Low-Performer), werden die neuen 12 Netzwerke für die neue Generation mit neu erzeugten Kindnetzwerken aufgefüllt („crossover“)! Jedes Kindnetzwerk übernimmt per Zufall einige Parameter vom Vaternetzwerk (z. B. Anzahl der Schichten) und den Rest der Parameter vom Mutternetzwerk – Kinder der gleichen Eltern sind somit „genetisch“ durch Zufallsauswahl der Parameter verschieden.
- Im letzten Schritt werden auch per Zufall einige dieser Netzwerke mutiert, das heißt, dass einige Hyperparameter neue Zufallswerte bekommen
In Abbildung 4 ist der Algorithmus grafisch dargestellt.
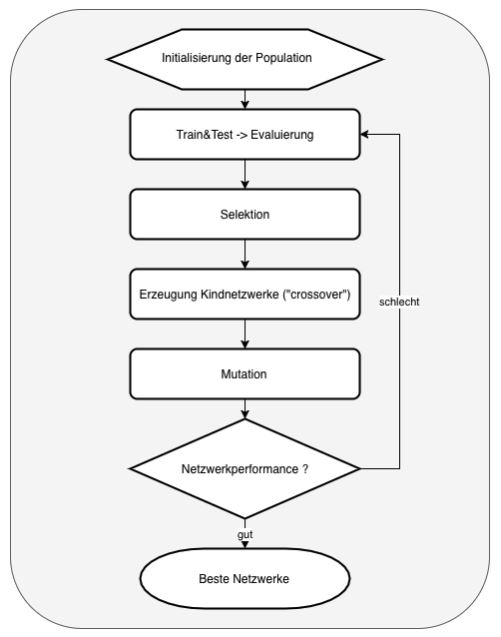
Abb. 4: Der genetische Algorithmus
Der genetische Algorithmus in unserem Java-DeepLearning4J-Netzwerk
Nachdem nun definiert ist, wie ein genetischer Algorithmus das beste Netzwerk finden kann, kann mittels DL4J dieser implementiert werden. In Listing 2 wird dazu eine Klasse Network definiert, welche einige zugewiesene Hyperparameter beinhaltet. Mittels der Methode createRandom werden einige Zufallsparameter für das Netzwerk generiert. Durch getAccuracy wird die Fitness-Funktion zur Verfügung gestellt, um später die besten Netzwerke auswählen zu können. Das Training des Netzwerks wird an die Klasse NetworkTraining in Listing 3 delegiert. Diese beinhaltet die DL4J-Implementierung.
public class Network {
private double accuracy;
private Hashtable nn_param_choices;
private Hashtable network_config;
public Network(Hashtable nn_param_choices) {
this.nn_param_choices = nn_param_choices;
this.network_config = new Hashtable();
accuracy = 0.0;
}
public void createRandom() {
List nb_neuronsChoices =
(List) this.nn_param_choices.get("nb_neurons");
List nb_layersChoices =
(List) this.nn_param_choices.get("nb_layers");
List activationChoices =
(List) this.nn_param_choices.get("activation");
List optimizerChoices =
(List) this.nn_param_choices.get("optimizer");
this.network_config.put("nb_neurons", nb_neuronsChoices.get(
new Random().nextInt(nb_neuronsChoices.size())));
this.network_config.put("nb_layers", nb_layersChoices.get(
new Random().nextInt(nb_layersChoices.size())));
this.network_config.put("activation", activationChoices.get(
new Random().nextInt(activationChoices.size())));
this.network_config.put("optimizer", optimizerChoices.get(
new Random().nextInt(optimizerChoices.size())));
}
public double getAccuracy() {
return this.accuracy;
}
public void train(DataSetIterator mnistTrain,
DataSetIterator mnistTest) {
NetworkTraining trainer = new NetworkTraining();
this.accuracy = trainer.train_and_score(
this, mnistTrain, mnistTest );
}
}public class NetworkTraining {
public MultiLayerNetwork compileNetwork(Network netConf) {
int nb_layers = (int) netConf.getConfig().get("nb_layers");
int nb_neurons = (int) netConf.getConfig().get("nb_neurons");
Activation activation =
(Activation) netConf.getConfig().get("activation");
OptimizationAlgorithm optimizer =
(OptimizationAlgorithm) netConf.getConfig().get("optimizer");
NeuralNetConfiguration.ListBuilder builder =
new NeuralNetConfiguration.Builder()
.seed(rngSeed) //include a random seed for reproducibility
.updater(new Nesterovs(0.006, 0.9)).l2(1e-4)
.optimizationAlgo(optimizer)
.list().layer(0, new DenseLayer.Builder()
.nIn(numRows * numColumns).nOut(nb_neurons)
.activation(activation).weightInit(WeightInit.XAVIER)
.build());
if (nb_layers > 1) { // Add layers between
builder.layer(0, new DenseLayer.Builder()
.nIn(nb_neurons).nOut(nb_neurons).activation(activation)
.weightInit(WeightInit.XAVIER)
.build());
} // Output Layer
builder.layer(1, new OutputLayer.Builder(
LossFunctions.LossFunction.NEGATIVELOGLIKELIHOOD)
.nIn(nb_neurons).nOut(outputNum).activation(Activation.SOFTMAX)
.weightInit(WeightInit.XAVIER)
.build());
MultiLayerConfiguration conf = builder.build();
MultiLayerNetwork model = new MultiLayerNetwork(conf);
model.init();
return model;
}
public double train_and_score(Network netConfig,
DataSetIterator mnistTrain, DataSetIterator mnistTest) {
MultiLayerNetwork networkModel = this.compileNetwork(netConfig);
int numEpochs = 15;
IntStream.range(0, numEpochs).mapToObj(
i -> mnistTrain).forEach(networkModel::fit);
//create an evaluation object with 10 possible classes:
Evaluation eval = new Evaluation(10);
while(mnistTest.hasNext()){
DataSet next = mnistTest.next();
//get the networks prediction:
INDArray output = networkModel.output(next.getFeatures());
//check the prediction against the true class:
eval.eval(next.getLabels(), output);
}
return eval.accuracy();
}
}Wie in Listing 3 zu sehen ist, erstellt die Methode compileNetwork ein neues DL4J-Netzwerk, wie es in der Konfiguration mit dem Parameter netConf übergeben wird. Man erkennt zum Beispiel am Parameter nb_layers, wie mehrere Schichten anhand der gewünschten Anzahl aufgebaut werden. Die Methode train_and_score trainiert das Netzwerk mit dem Trainingsdatensatz und gibt die Genauigkeit („accuracy“) zurück, welche über den Testdatensatz ermittelt wurde – in unserem Fall ist das der Fitnesscore für den genetischen Algorithmus.
Damit ist nun die Grundlage für den Algorithmus gelegt. Die Klasse Optimizer in Listing 4 implementiert die in der Einleitung erwähnten Konzepte. Eine neue Population von Netzwerken mit Zufallswerten wird mit der Methode createPopulation zur Verfügung gestellt. Das Erzeugen von neuen Kindelementen übernimmt die Methode breed – es werden zwei Kindnetzwerke aus zwei zufälligen Eltern der Population erzeugt, die übernommenen Werte der Eltern sind selbst auch zufällig.
Eine notwendige Mutation bietet die Methode mutate, es werden zufällig einige Hyperparameter des Netzwerks mutiert. Nun kann sich die aktuelle Population von Netzwerken in der Methode evolve weiterentwickeln, aus der gesamten Population werden nur die High-Performer und ein paar Low-Performer übernommen. Die restlichen Plätze der Population werden mit neuen Kindnetzwerken aufgefüllt – somit ist die neue Generation erzeugt.
Nachdem nun die Bausteine des Algorithmus zur Verfügung stehen, wird wie in Listing 5 eine initiale Population erzeugt und in der Methode generate jedes Netzwerk in einer Population trainiert sowie gemessen, wie gut es abschneidet. Danach wird die gesamte Population mittels evolve in eine neue Generation per Evolution weiterentwickelt.
Im Vergleich zu einem reinem Brute-Force-Ansatz, bei dem als Beispiel eine Genauigkeit („accuracy“) von 56 Prozent in ca. 63 Stunden erreicht wird, braucht der genetische Ansatz nur ca. 7 Stunden, um das gleiche Netzwerk mit der gleichen Performanz zu finden. Je besser die Population mit mehreren Generationen fortgeschritten ist, desto besser lassen sich inkrementelle Verbesserungen der Netzwerkperformanz erreichen.
public class Optimizer {
public List<Network> createPopulation(int count) {
List<Network> result = new ArrayList<>();
IntStream.range(0, count).mapToObj(i ->
new Network(this.nn_param_choices))
.forEach(netConfig -> {
netConfig.createRandom(); result.add(netConfig); });
return result;
}
public static double fitness(Network network) {
return network.getAccuracy();
}
public List<Network> breed(Network father, Network mother) {
// Randomly mutate some children:
List<Network> twoChildren = new ArrayList<>();
IntStream.range(0, 2).mapToObj(
i -> new Network(this.nn_param_choices)).forEach(child -> {
Hashtable config = new Hashtable();
config.put("nb_neurons", getRandomFatherOrMother(father, mother)
.getConfig().get("nb_neurons"));
// ... copy others
if (mutate_chance > Math.random()) { mutate(child); }
twoChildren.add(child);
});
return twoChildren;
}
public void mutate(Network network) {
List<String> keys =
Arrays.asList("nb_neurons", "nb_layers",
"activation", "optimizer");
String randomHyperParameterKey =
keys.get(new Random().nextInt(keys.size()));
List hyperParameterValues =
(List) this.nn_param_choices.get(randomHyperParameterKey);
network.getConfig().put(
randomHyperParameterKey, hyperParameterValues.get(
new Random().nextInt(hyperParameterValues.size())));
}
public List<Network> evolve(List<Network> population) {
List<Network> strongestNetworks =
orderStrongestNetworks(population);
// Get the number we want to retain for the next generation
int retain_length = (int) (population.size() * this.retain);
// Survivors will go to the next generation
List<Network> survivors =
strongestNetworks.subList(0, retain_length);
// Keep some random low performers from the end of the strongest
for (int i=strongestNetworks.size();
i>strongestNetworks.size() - retain_length; i--) {
if (this.random_select > Math.random()) {
survivors.add(strongestNetworks.get(i));
}
}
// If there are some free spots for the next generation,
// fill them up with children
int newChildrenLength = population.size() - survivors.size();
List<Network> children = new ArrayList<>();
while (children.size() < newChildrenLength) {
int fatherIndex = new Random().nextInt(survivors.size());
int motherIndex = new Random().nextInt(survivors.size());
if (fatherIndex != motherIndex) {
List<Network> twoKids =
breed(survivors.get(fatherIndex), survivors.get(motherIndex));
for (Network kid : twoKids) {
if (children.size() < newChildrenLength) {
children.add(kid);
...
survivors.addAll(children);
return survivors;
...public class EvolutionExecuter {
public static void main(String[] args) throws Exception {
int generations = 2; int population = 20;
Hashtable nn_param_choices = new Hashtable();
nn_param_choices.put("nb_neurons", Arrays.asList(
64, 128, 256, 512, 768, 1024));
nn_param_choices.put("nb_layers", Arrays.asList(1, 2, 3, 4));
nn_param_choices.put("activation", Arrays.asList(
Activation.RELU, Activation.LEAKYRELU,
Activation.TANH, Activation.SOFTMAX));
nn_param_choices.put("optimizer", Arrays.asList(
OptimizationAlgorithm.LINE_GRADIENT_DESCENT,
OptimizationAlgorithm.STOCHASTIC_GRADIENT_DESCENT));
EvolutionExecuter executor = new EvolutionExecuter();
executor.generate(generations, population, nn_param_choices);
}
public void generate(int generationCount, int populationCount,
Hashtable nn_param_choices) throws IOException {
int rngSeed = 123; // random number seed for reproducibility
int batchSize = 64; // batch size for each epoch
DataSetIterator mnistTrain =
new MnistDataSetIterator(batchSize, true, rngSeed);
DataSetIterator mnistTest =
new MnistDataSetIterator(batchSize, false, rngSeed);
Optimizer networkOptimizer =
new Optimizer(nn_param_choices, 0.4, 0.1, 0.2 );
List<Network> population =
networkOptimizer.createPopulation(populationCount);
int i=0; // Evolve multiple generations
while (i<generationCount) { // Train network population
trainNetworkPopulation(population, mnistTrain, mnistTest);
if (i <= generationCount -1) {
population = networkOptimizer.evolve(population);
}
i++;
} // Sort the final population
population = networkOptimizer.orderStrongestNetworks(population);
}
public void trainNetworkPopulation(List<Network> population,
DataSetIterator mnistTrain, DataSetIterator mnistTest) {
for (Network network : population) {
network.train(mnistTrain, mnistTest);
}
}
}Fazit und Ausblick
Die Ergebnisse, die mittels der DL4J-Implementierung und dem genetischen Algorithmus erreicht wurden, sind beeindruckend. Durch verschiedene Mechanismen, die der Evolution in der Natur nachempfunden sind, können bessere KI-Architekturen entstehen, die selbst von Maschinen erstellt und optimiert werden – dies ist ein wichtiger Bestandteil für die Ausbreitung und Entwicklung von Künstlicher Intelligenz und letztendlich ein Eckpfeiler des selbstorganisierenden Lebens.
Der komplette Quellcode zu dem MNIST-Beispiel ist unter [Git-Hub] zu finden.
Links
[AutoKeras]
G. Seif, AutoKeras: The Killer of Google’s AutoML, Towards Data Science, 31.7.2018,
https://towardsdatascience. com/autokeras-the-killer-of-googles-automl-9e84c552a319
[AutoML]
J. Hu, Understanding AutoML and Neural Architecture Search, AI Frontiers, 17.9.2018,
https://medium.com/aifrontiers/understand-automl-and-neural-architecture-search-4260a0942116
[Bayesian]
B. Letham u.a., Efficient tuning of online systems using Bayesian optimization, Facebook Research, 17.9.2018, https://research.fb.com/efficient-tuning-of-online-sys temsusing-bayesian-optimization/
[GitHub]
https://github.com/juergen1976/GeneticNeuralNetworks
[NeuralNets]
M. A. Nielsen, Neural Networks and Deep Learning, Determination Press, 2015, Kapitel 1,
http://neuralnetworksanddeeplearning.com/chap1.html