Das Ziel eines jeden Softwareentwicklers ist es, Programme mit möglichst wenigen Fehlern zu schreiben. Dabei helfen erstens konstruktive Maßnahmen. Dazu gehört die Einhaltung von Programmierrichtlinien ebenso wie das Schreiben eines verständlichen, wartungsfreundlichen Programmtextes. Zweitens hilft das Testen, also die Prüfung der Software, ob sie den Anforderungen genügt und ob sie Fehler enthält. Aber: Wie prüfe ich mein Programm(teil) auf Fehler und wie groß darf ein vertretbarer Testaufwand sein?
Einerseits soll möglichst wenig Aufwand in den Test gesteckt werden, um die Kosten niedrig zu halten, andererseits möglichst viel, um dem Ziel der Fehlerfreiheit nahezukommen. Letztlich geht es darum, einen vernünftigen Kompromiss zwischen diesen beiden Extremen zu finden. Der aus dem agilen Umfeld bekannte Begriff „lean“ bedeutet beim Testen, sich auf das Wichtige zu konzentrieren, um diesen Kompromiss zu erreichen.
Um mit wenig Testeinsatz viel überprüfen zu können, muss der Code – das Testobjekt – möglichst einfach sein. Glücklicherweise hat sich in den letzten Jahren ein Wandel hin zum einfachen guten Programmierstil ergeben. Die Beachtung der Clean-Code-Prinzipien schafft eine wichtige Voraussetzung, den Test angemessen aufwendig gestalten zu können.
Brücke zwischen Programmierung und Test
Jeder Softwareentwickler testet seinen Code und möchte gute Software abliefern. Er muss aber auch darauf achten, nicht mehr Zeit als angemessen zu investieren. Die aktuelle Entwicklung, bei der Softwareerstellung keine strikte (personenbezogene) Trennung zwischen Implementierung und Test auf Unit-Ebene vorzusehen, erfordert eine Brücke zwischen Programmierung und Testen für den Entwickler. Ihm soll bekannt sein, welche Testverfahren es gibt und wie sie mit vertretbarem Aufwand auf seiner Ebene eingesetzt werden können.
Mit dem Begriff „Lean Testing“ möchten wir verdeutlichen, dass das Testen nicht zwangsläufig mit hohem Aufwand und mit vielen Testfällen verknüpft ist. Durch die systematische Verwendung von Testverfahren, die der Tester kennt und einsetzt, ist es auch dem Entwickler möglich, die Prüfung seiner Software effektiv und effizient durchzuführen – eben „lean“. Wir möchten das Vorgehen an den folgenden zwei Beispielen erörtern.
Lean Testing 1: Von 27 zu 13 Testfällen
Es sei eine (fehlerhafte) Java-Funktion zum Finden des maximalen Werts dreier Zahlen gegeben (nach [Kle13]):
public static int max(int x, int y, int z) { int max=0; if(x>z) max=x; if(y>x) max=y; if(z>y) max=z; return max;}
Sicherlich sehen Sie bereits, dass dieses Programmstück seine Tücken hat. Da in Java ein int-Wert 32 Bits hat, ergibt sich eine riesige Zahl möglicher Eingabekombinationen (296). Offensichtlich ist es sinnlos, diese Kombinationen alle testen zu wollen. Nehmen wir nun weiter an, wir entscheiden uns dafür, den Test mit nur drei Testfällen durchzuführen. Bei jedem Testfall wird der zu ermittelnde Maximalwert durch einen anderen Parameter übergeben. Dies scheint eine sinnvolle Wahl von Testfällen zu sein, wenn das Maximum ermittelt werden soll.
Man könnte nun auf die Idee kommen, einfach drei verschiedene Zahlen herauszugreifen und die Funktion damit zu testen, zum Beispiel 4, 5 und 7. Die Tests mit max(4,5,7), max(5,7,4) und max(7,5,4) sind alle erfolgreich. Darüber hinaus wird jede Entscheidung mit true und false ausgewertet. Wir haben also 100 Prozent Entscheidungsüberdeckung! Tatsächlich ist das nicht ausreichend, schon max(7,4,5) schlägt fehl.
Besser systematisch als ad hoc
Anstelle des Ad-hoc-Vorgehens ist ein systematisches Vorgehen sinnvoll. Dazu wird angenommen, dass die Funktion bei jeder ganzen Zahl korrekt arbeitet, ob sie nun 9999 oder -3 ist. Das heißt, die Zahlen sind äquivalent. Damit reichen tatsächlich drei konkrete Zahlen aus. Aus diesen lassen sich dann 33 = 27 Kombinationen bilden – schon erheblich weniger als 296.
Eine weitere Reduktion ergibt sich aus der Überlegung, dass es beim Finden des Maximums nur um die relativen Größenverhältnisse geht. Das führt auf die folgenden Testfälle:
- Alle Zahlen sind gleich, ein möglicher Repräsentant für ein zu testendes Tripel ist 7, 7, 7.
- Zwei Zahlen sind gleich und die dritte ist größer: 7, 5, 5; 5, 7, 5; 5, 5, 71.
- Zwei Zahlen sind gleich und die dritte ist kleiner: 7, 7, 5; 7, 5, 7; 5, 7, 7.
- Alle Zahlen sind ungleich: 7, 5, 4; 7, 4, 5; 5, 7, 4; 4, 7, 5; 4, 5, 7; 5, 4, 7.
In der Summe ergeben sich nun vier Gruppen von Klassen äquivalenter Werte. Das heißt, dass sich die Funktion bei jedem Zahlentripel einer Klasse gleich verhält. Solche Klassen heißen Äquivalenzklassen. Unter möglicher Repräsentant wird ein konkreter Fall von mehreren einer Äquivalenzklasse verstanden: Statt 7, 7, 7 wäre auch 4, 4, 4 oder 5, 5, 5 möglich. Es gibt nun insgesamt 13 Testfälle. Sie enthalten auch die Fälle, bei denen die Funktion scheitert. Werte in Äquivalenzklassen zu unterteilen, liegt hier nahe.
Bei der Unterteilung in Äquivalenzklassen ist es im Allgemeinen erforderlich, auch ungültige Werte zu betrachten, also Werte, bei denen eine Funktion auf jeden Fall scheitern muss. Hierauf wird aber in diesem Beitrag nicht näher eingegangen.
Die Aufteilung in Äquivalenzklassen ist nur ein Weg, systematisch an das Testen heranzugehen.
Lean Testing 2: Von 16 zu 5 und von 1024 zu 13 Testfällen
Sehen wir uns ein weiteres Vorgehen zur Erstellung von Testfällen an. Bei Funktionen kommt es häufig vor, dass Parameter unabhängig voneinander sind und unterschiedliche Werte annehmen können. Die Frage, die sich beim Testen stellt, ist, „Welche Werte der Parameter sollen miteinander kombiniert werden?“ Auf der sicheren Seite ist man, wenn alle Werte miteinander kombiniert werden. Dies übersteigt in aller Regel aber den vertretbaren Aufwand. Was wäre nun ein Lean-Testing-Ansatz?
2er-Kombinationen bei 4 booleschen Parametern
Nehmen wir ein einfaches Beispiel mit vier booleschen Parametern A, B, C und D zur Verdeutlichung. Es ergeben sich 24 = 16 Kombinationen. Sehen wir uns die fünf Kombinationen beziehungsweise Testfälle in Tabelle 1 an.
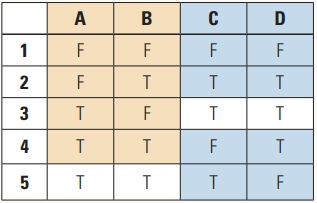
Tabelle 1: Kombinationen mit vier booleschen Parametern
Die fünf Testfälle scheinen relativ willkürlich aus den 16 möglichen gewählt zu sein. Jeder Parameter erhält beide booleschen Werte – schon mal ein erster sinnvoller Ansatz! Aber dafür würden auch zwei Testfälle (alle Parameterwerte einmal T-true und einmal F-false) ausreichen.
Betrachten wir nun die einzelnen Kombinationen der jeweiligen Parameterpaare, also Parameter A mit Parameter B (farblich hervorgehoben), A mit C, …, C mit D (farblich hervorgehoben).
Fällt Ihnen etwas auf? Auf die Parameterpaare bezogen kommen alle vier möglichen Kombinationen (TT, TF, FT, FF) in den fünf Testfällen vor! Das ist ein Lean-Testing-Ansatz: Nicht alle 16 möglichen Kombinationen, sondern eine sinnvolle, nachvollziehbare Auswahl von Testfällen wird zum Testen herangezogen. Die Ersparnis ist in diesem Beispiel nicht sehr groß – von 16 auf 5. Dies liegt aber daran, dass es bei den Parametern nur zwei Möglichkeiten (true, false) gibt und die Anzahl der Parameter gering ist.
3er-Kombinationen bei 10 booleschen Parametern
Nehmen wir ein umfangreicheres Beispiel mit 10 booleschen Parametern zur weiteren Klärung des Ansatzes. Es ergeben sich 210 = 1024 Kombinationen – zu viele! Sehen wir uns die 13 Kombinationen beziehungsweise Testfälle aus Tabelle 2 an.
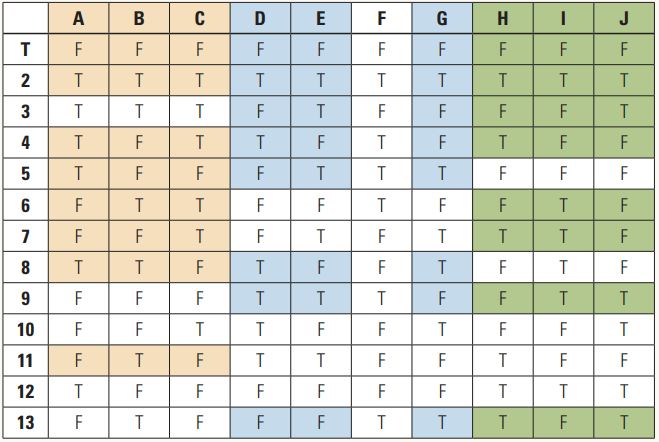
Tabelle 2: Kombinationen mit zehn booleschen Parametern (Beispiel in Anlehnung an [Kuh10])
Es geht hier nicht mehr um Paare von Parametern, die miteinander vollständig kombiniert werden, sondern es sind Tripel. Drei beliebige verschiedene Spalten enthalten alle acht möglichen Kombinationen für drei binäre Variablen! In der Tabelle sind einige Spalten entsprechend farbig markiert, man könnte aber auch beliebige andere drei Spalten kombinieren, etwa F, G und H. Es werden immer alle acht Möglichkeiten mit den 13 Testfällen abgedeckt.
Das hier skizzierte Verfahren gehört zu den kombinatorischen Testverfahren [Kuh10]. Grundlage sind sogenannte Covering Arrays. Mit dem Verfahren kann die Anzahl der Testfälle variiert werden, je nach geforderter Intensität des Testens. Die Anzahl bleibt aber immer noch weit unter der Anzahl, als wenn alle möglichen Kombinationen herangezogen werden.
Das ist „Lean Testing“! Nicht alle möglichen Kombinationen, sondern eine sinnvolle, nachvollziehbare Auswahl von Testfällen wird zum Testen verwendet. Die Idee ist dabei, dass es meistens nur begrenzte Abhängigkeiten der Parameter untereinander gibt und dass man die meisten Fehler findet, wenn die Parameter wie beschrieben variiert und kombiniert werden. Das Vorgehen wird in [Spi16] ausführlich beschrieben und es wird eine Werkzeugunterstützung vorgestellt, welche die entsprechenden Kombinationen erzeugt.
Fazit
Wir haben zwei Beispiele zum „Lean Testing“ vorgestellt und damit verdeutlicht, dass bei systematischem Vorgehen mit wenig Aufwand ein angemessener Test durchgeführt werden kann.
In [Spi16] finden sich weitere Verfahren mit ausführlichen Beispielen (die alle zum Download zur Verfügung stehen, allerdings in C++), um den richtigen Mittelweg zwischen zu wenig und zu viel Testen herauszufinden. Es werden Testverfahren angesprochen, die zwar dem professionellen Tester gut bekannt sind, nicht jedoch vielen Softwareentwicklern. Diesen soll eine Handreichung für die tägliche Arbeit gegeben werden, ganz im Sinn der oben angesprochenen Brücke zwischen Programmierung und Testen.
Referenzen
[Kle13]
St. Kleuker, Qualitätssicherung durch Softwaretests, Springer Vieweg, 2013
[Kuh10] D. R. Kuhn, R. N. Kacker, Yu Lei, Practical Combinatorial Testing, National Institute of Standards and Technology (NIST), 2010 (siehe:
http://dx.doi.org/10.6028/NIST.SP.800-142)
[Spi16]
A. Spillner, U. Breymann, Lean Testing für C++-Programmierer, dpunkt.verlag, 2016 (siehe auch http://www.leantesting.de/)1
1) Teile des Beitrags sind dem Buch [Spi16] entnommen.