Development Java

Das Fork-Join-Framework

Das Fork-Join-Framework ist seit Version 7 fester Bestandteil von Java. Um seine großen Vorteile zu demonstrieren, werden in diesem Artikel zeit- und rechenintensive Szenarien aufgesetzt und in einem einzelnen Thread, in einem Thread-Pool fixer Größe und auf zwei Arten mithilfe des Fork-Join-Frameworks abgearbeitet und miteinander verglichen.

Christian Heitzmann

Author

27.09.2019
Lesezeit: 11 Minuten
94 Views

Die Beispiele, die sich in der deutschsprachigen Java-Populärliteratur zum Fork-Join-Framework finden lassen, sind nicht sehr überzeugend. Fakultäten oder Fibonacci-Zahlen rekursiv zu berechnen und diese dann mittels Fork-Join-Algorithmen zu optimieren, behebt einfach nur künstliche Probleme, die gar nicht erst hätten entstehen dürfen. Das Gleiche gilt für die Multiplikation großer Zahlen durch wiederholtes Addieren. Was in all diesen Beispielen fehlt, sind richtig lange Berechnungen. Aus diesem Grund sollen zuerst lange Berechnungen eingeführt werden.

Lange Berechnungen und Werte mit Zeitstempel

Die Klasse LengthyComputation (s. Listing 1) wird für alle folgenden Codebeispiele verwendet. Sie enthält nur eine statische Methode computeValue(int passCount), die eine einzelne Zahl durch 10 000-fache Anwendung eines linearen Kongruenzgenerators (englisch: linear congruential generator, LCG) berechnet. Der LCG implementiert ein gebräuchliches Verfahren, um sogenannte Pseudozufallszahlen zu erzeugen [Heitz19].

import java.util.concurrent.*;
public final class LengthyComputation {
private static final int SEQUENCE_LENGTH = 10_000;
private static final int A = 1_664_525;
private static final int C = 1_013_904_223;
private LengthyComputation() {}
public static int computeValue(int passCount) {
 int value = ThreadLocalRandom.current().nextInt();
 for (int passNumber = 1; passNumber <= passCount; passNumber++) {
 for (int i = 1; i <= SEQUENCE_LENGTH; i++) {
 value = A * value + C;
 }
 }
 return value;
}
}

Listing 1: Flexibel lange Berechnung

Der Entscheid, für die folgenden Beispiele einen LCG zu verwenden, gründet auf seiner Eigenschaft, damit „unendlich lange“ Berechnungen durchführen zu können. Durch Übergeben einer positiven Zahl an passCount kann der Aufrufer steuern, wie lange die Berechnung dauern soll. So wird zum Beispiel der Methodenaufruf computeValue(1000) 10-mal länger dauern als der Methodenaufruf mit dem Parameter 100. Für reale Anwendungen kann LengthyComputation einfach durch eine eigene lange Berechnung ausgetauscht werden. Um das Verhalten der verschiedenen Berechnungsarten, die in diesem Artikel vorgestellt werden, beobachten zu können, werden die Szenarios immer darin bestehen, ein Array der Größe 10 000 mit Werten zu füllen, die man aus den oben beschriebenen „langen Berechnungen“ erhält. Zusätzlich wird jeder berechnete Wert zusammen mit einem Zeitstempel gespeichert, der die Zeit seit dem Start der Applikation angibt. Die entsprechende Datenstruktur in Listing 2 ist trivial.

import java.time.*;
import java.util.*;
public final class TimestampedValue {
private int value;
private Duration timestamp;
public TimestampedValue(int value, Duration timestamp) {
 Objects.requireNonNull(timestamp);
this.value = value;
this.timestamp = timestamp;
}
public int getValue() {
 return value;
}
public Duration getTimestamp() {
 return timestamp;
}
}

Listing 2: Wert mit Zeitstempel

Allerdings fehlt noch eine wichtige Sache: Würde jeder der 10 000 Array-Werte auf die gleiche Art berechnet, so würde jede der 10 000 Berechnungen auch mehr oder weniger die gleiche Zeit in Anspruch nehmen. Das ist nicht sehr realistisch, unterscheiden sich die Problemgrößen in der echten Welt normalweise doch recht deutlich voneinander. Es würde auch nicht die Vorteile des Fork-Join-Frameworks demonstrieren, denn dieses würde vermutlich nicht besser performen, als wenn man das Array einfach in n Teile zerlegen und n unabhängige Threads parallel daran arbeiten lassen würde (wobei n üblicherweise der Anzahl der CPU-Kerne entsprechen sollte).

Aus diesem Grund wird die Berechnung des Array-Elementes am Index 0 in der computeValue-Methode 0 Durchläufe vornehmen, die Berechnung des Array-Elementes mit Index 5000 wird 5000 Durchläufe durchmachen, und die Berechnung am Index 9999 wird 9999-mal durchlaufen. Das Füllen des Arrays mit 10 000 berechneten Werten wird daher sehr asymmetrisch ablaufen, da Berechnungen für große Indizes länger dauern als Berechnungen für kleine.

Berechnung in einem einzelnem Thread

Die Klasse SingleThreadComputation in Listing 3 berechnet alle 10 000 Elemente von array auf triviale Art. Sie besteht aus einem einzelnen Thread. Eine einfache Schleife iteriert alle Indizes von 0 bis 9999, ruft die computeValue-Methode auf (wobei es arrayIndex als passCount verwendet, wie oben beschrieben) und speichert ihren Wert zusammen mit dem aktuellen Zeitstempel. Ist PRINT_MESSAGES = true, dann lässt sich der Fortschritt des Array-Füllens anzeigen. Zu Beginn ist es sehr schnell und wird dann über den gesamten Bereich zunehmend langsamer.

import java.time.*;
public final class SingleThreadComputation {
private static final boolean PRINT_MESSAGES = true;
// private static final boolean PRINT_MESSAGES = false;
private static final int ARRAY_SIZE = 10_000;
private TimestampedValue[] array = new TimestampedValue[ARRAY_SIZE];
public static void main(String[] args) {
SingleThreadComputation computation = new SingleThreadComputation();
 computation.compute();
 // computation.printTimestamps();
}
private void compute() {
Instant startTime = Instant.now();
for (int arrayIndex = 0; arrayIndex < ARRAY_SIZE; arrayIndex++) {
 if (PRINT_MESSAGES) {
 if ((arrayIndex % 10) == 0) {
 System.out.format("Computing values for indexes "
 + "%4d to %4d.%n",
 Integer.valueOf(arrayIndex),
 Integer.valueOf(Math.min(arrayIndex + 9,
 ARRAY_SIZE - 1)));
 }
 }
 int value = LengthyComputation.computeValue(arrayIndex);
 Duration timestamp = Duration.between(startTime, Instant.now());
 array[arrayIndex] = new TimestampedValue(value, timestamp);
 }
}
private void printTimestamps() {
for (int arrayIndex = 0; arrayIndex < ARRAY_SIZE; arrayIndex++) {
 System.out.println(arrayIndex + "\t"
 + array[arrayIndex].getTimestamp().toMillis());
 }
}
}

Listing 3: Berechnung in einem einzelnen Thread

Auf meiner Maschine (MacBook Pro mit einem 2,8 GHz Intel Core i7) dauert die gesamte Berechnung etwa 566 s, das heißt etwa 9,4 min. Abbildung 1 zeigt die Zeitstempel jedes array-Elementes und illustriert dabei perfekt das parabolische Zeitverhalten der linear zunehmenden Berechnungsdauern pro Element.

Um all die Diagramme aus diesem Artikel reproduzieren zu können, kann man die entsprechenden Methodenaufrufe computation. printTimestamps() entkommentieren. Sie geben eine unformatierte Liste von Array-Index-Zeitstempel-Paaren aus. Wird die Konsolenausgabe in eine Datei umgeleitet und mit einem Plot-Programm der Wahl dargestellt, wird man ähnliche Resultate erhalten.

Berechnung in einem Thread-Pool fixer Größe

Mit den Concurrency Utilities, die in Java 5 eingeführt wurden, kamen auch verschiedene Typen von Thread-Pools [JAPIExec]. Sie machen den manuellen Umgang mit Threads praktisch überflüssig. Anstatt mit wait, notify und notifyAll herumzudoktern, verwendet man besser einen der bereitgestellten Thread-Pools. Ein solcher Pool enthält – in seiner grundlegenden Form – eine Warteschlange, die alle übermittelten Tasks enthält (quasi eine „To-Do-Liste“ von Tasks), sowie mehrere sogenannte Worker-Threads, die die Tasks aus der Queue entnehmen und ausführen. Der Hauptvorteil eines Thread-Pools besteht in seiner Fähigkeit, Worker-Threads wiederzuverwenden, wodurch der Overhead, der durch das Erzeugen und Entfernen von Threads entsteht, weitestgehend entfällt.

Die Anzahl Worker-Threads kann entweder fix oder dynamisch sein, abhängig vom Typ des Thread-Pools. Executors.newFixedThread-Pool(int) gibt einen ExecutorService mit einer fixen Anzahl an Worker-Threads zurück. Idealerweise setzt man die Anzahl Worker-Threads gleich der Anzahl CPU-Kerne im System, wozu die Methode Runtime.getRuntime().availableProcessors() eine perfekte Hilfe bietet.

Um die Berechnung aller array-Werte zu beschleunigen, unterteilt das Codebeispiel in Listing 4 das Array in THREAD_COUNT (auf meiner Maschine: 8) Teil-Arrays und reicht dem Thread-Pool anschließend entsprechend viele Berechnungs-Tasks ein, wobei jeder Task (auf meiner Maschine) 1/8 des Arrays berechnet.

import java.time.*;
import java.util.concurrent.*;
public final class FixedThreadPoolComputation {
private static final int ARRAY_SIZE = 10_000;
private static final int THREAD_COUNT
 = Runtime.getRuntime().availableProcessors();
private TimestampedValue[] array = new TimestampedValue[ARRAY_SIZE];
private Instant startTime;
public static void main(String[] args) throws InterruptedException {
 FixedThreadPoolComputation computation
 = new FixedThreadPoolComputation();
 computation.setUpAndSubmitComputation();
 // computation.printTimestamps();
}
private void setUpAndSubmitComputation() throws InterruptedException {
startTime = Instant.now();
 ExecutorService service
 = Executors.newFixedThreadPool(THREAD_COUNT);
for (int threadNumber = 1;
threadNumber <= THREAD_COUNT;
 threadNumber++) {
final int indexMinInclusive
 = ARRAY_SIZE * (threadNumber - 1) / THREAD_COUNT;
final int indexMaxExclusive
 = ARRAY_SIZE * threadNumber / THREAD_COUNT;
service.submit(() -> compute(indexMinInclusive,
 indexMaxExclusive));
}
service.shutdown();
while (!service.awaitTermination(1, TimeUnit.MINUTES)) {}
}
private void compute(int indexMinInclusive, int indexMaxExclusive) {
for (int arrayIndex = indexMinInclusive;
 arrayIndex < indexMaxExclusive;
 arrayIndex++) {
 int value = LengthyComputation.computeValue(arrayIndex);
 Duration timestamp = Duration.between(startTime, Instant.now());
 array[arrayIndex] = new TimestampedValue(value, timestamp);
 }
}
/* [...] Method printTimestamps() omitted. */
}

Listing 4: Berechnung in einem Thread-Pool fixer Größe

Wenn alle Elemente die gleiche Berechnungszeit bräuchten, dann wäre das Array in 1/8 der Zeit gefüllt. Wie allerdings weiter oben ausgeführt wurde, nehmen die Berechnungszeiten mit zunehmender Indexgröße zu. So hat der 8. Thread, der die Werte für die Indizes 8750 bis 9999 berechnet, viel mehr Arbeit als der 1. Thread, der von Index 0 bis 1249 berechnet. Abbildung 2 bestätigt diese Annahme.

Die Gesamtzeit bei Benutzung eines Thread-Pools mit fixer Größe beträgt auf meiner Maschine 132 s, das heißt 2,2 min, und ist damit mehr als 4-mal schneller als die Berechnung in einem einzelnen Thread aus dem vorherigen Abschnitt.

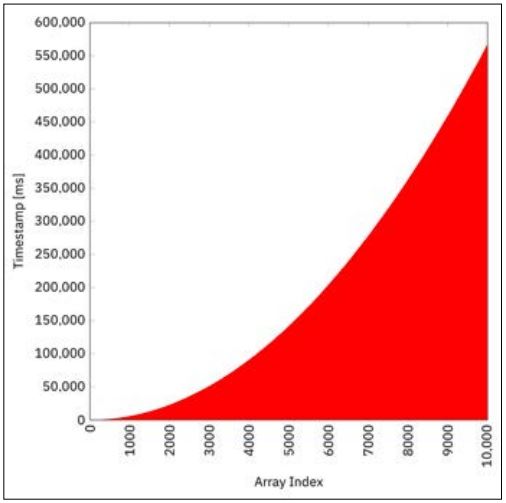
Abb. 1: Berechnung in einem einzelnen Thread

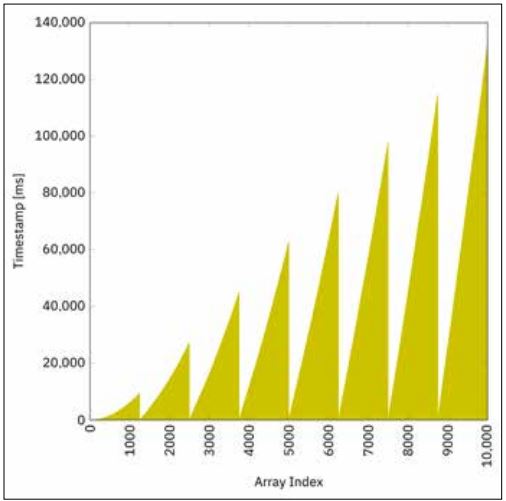
Abb. 2: Berechnung in einem Thread-Pool fixer Größe

Fork-Join-Pool mit Invoke-All-Berechnung

Ein Fork-Join-Pool ist ein Thread-Pool, der für Aufgaben, die sich aufteilen lassen, konzipiert ist. Er folgt damit einer Teile-und-herrsche-Strategie (englisch: divide and conquer) [JAPIFork]. Wenn ein Problem zu groß ist, dann wird es in zwei kleinere Teile zerlegt. Wenn also das Füllen des arrays mit 10 000 Elementen kompliziert ist, vielleicht ist es das Füllen des Arrays mit „nur“ 5000 Elementen nicht mehr?

Nun, ist es immer noch, aber wenn die Problemgröße weiter und weiter geteilt wird, kommt man schließlich an einem Punkt an, an dem das Lösen des Problems trivial wird. Das ist definitiv der Fall, wenn nur noch ein array-Element zur Berechnung übrig ist, aber aus Optimierungsgründen gehen wir davon aus, dass die Berechnung von 10 Elementen ebenfalls noch als trivial bezeichnet werden kann. Listing 5 zeigt den ersten Teil des Codes, die InvokeAllComputationAction, die Javas RecursiveAction erweitert.

import java.time.*;
import java.util.*;
import java.util.concurrent.*;
@SuppressWarnings("serial")
public final class InvokeAllComputationAction
extends RecursiveAction {
private static final boolean PRINT_MESSAGES = true;
// private static final boolean PRINT_MESSAGES = false;
private static final int BASE_CASE_ELEMENT_COUNT_MAX = 10;
private static TimestampedValue[] array;
private static Instant startTime;
private int indexMinInclusive;
private int indexMaxExclusive;
public InvokeAllComputationAction(int indexMinInclusive,
 int indexMaxExclusive,
 TimestampedValue[] array,
 Instant startTime) {
 this(indexMinInclusive, indexMaxExclusive);
 Objects.requireNonNull(array);
 Objects.requireNonNull(startTime);
InvokeAllComputationAction.array = array;
InvokeAllComputationAction.startTime = startTime;
}
public InvokeAllComputationAction(int indexMinInclusive,
 int indexMaxExclusive) {
this.indexMinInclusive = indexMinInclusive;
this.indexMaxExclusive = indexMaxExclusive;
}
@Override
protected void compute() {
/* base case */
if ((indexMaxExclusive - indexMinInclusive)
 <= BASE_CASE_ELEMENT_COUNT_MAX) {
 if (PRINT_MESSAGES) {
 System.out.format("Computing base case for indexes "
 + "%4d to %4d.%n",
 Integer.valueOf(indexMinInclusive),
 Integer.valueOf(indexMaxExclusive - 1));
 }
 for (int arrayIndex = indexMinInclusive;
 arrayIndex < indexMaxExclusive;
 arrayIndex++) {
 int value = LengthyComputation.computeValue(arrayIndex);
 Duration timestamp = Duration.between(startTime, Instant.now());
 array[arrayIndex] = new TimestampedValue(value, timestamp);
 }
 /* recursive case */
} else {
 int indexMid = (indexMinInclusive + indexMaxExclusive) / 2;
 if (PRINT_MESSAGES) {
 System.out.format("Invoking recursive cases for indexes "
 + "%4d to %4d and %4d to %4d.%n",
 Integer.valueOf(indexMinInclusive),
 Integer.valueOf(indexMid - 1),
 Integer.valueOf(indexMid),
 Integer.valueOf(indexMaxExclusive - 1));
 }
 invokeAll(new InvokeAllComputationAction(indexMinInclusive,
 indexMid),
 new InvokeAllComputationAction(indexMid,
 indexMaxExclusive));
 }
}
}

Listing 5: Fork-Join-Pool mit Invoke-All-Berechnung

Das ganze Konzept basiert auf Rekursion. Der Rekursionsanfang ist der triviale Fall, der direkt berechnet werden kann, wie oben beschrieben. Sein Schwellenwert kann in der Konstanten BASE_CASE_ ELEMENT_COUNT_MAX gesetzt werden und ist initial auf 10 eingestellt.

Der Rekursionsschritt repräsentiert den „komplizierten“ Fall. Das aktuelle Teil-Array wird in zwei Hälften zerlegt. Zwei Invoke-AllComputationActions werden erzeugt, wobei jede einen Berechnungs-Task für eine der beiden Hälften repräsentiert. Der invoke-All-Aufruf am unteren Ende des Codes fügt diese zwei Tasks dann der Warteschlange hinzu.

Fork-Join-Pools sind optimiert in der Art, wie sie die eingereihten Tasks bearbeiten. Jeder Worker-Thread hat seine eigene lokale Warteschlange, zusätzlich zu einer einzigen globalen Warteschlange. Jeder Worker-Thread arbeitet sich zuerst durch seine eigene lokale Warteschlange. Wenn ein Worker-Thread seine eigene Queue geleert hat, wendet es Work Stealing an, das heißt, es „stiehlt“ Arbeit von einer anderen lokalen Queue.

Der invokeAll-Aufruf reiht neue Tasks in die Thread-eigene lokale Warteschlange ein. Tasks von der Queue des eigenen Threads werden nach LIFO-Art bearbeitet (Last In First Out, das heißt, der letzte Task kommt zuerst, wie bei einem Stack). Tasks von der Queue eines anderen Threads werden nach FIFO-Art abgearbeitet (First In First Out, das heißt, der älteste Task kommt zuerst, wie bei einer Pipeline). Letzteres gilt auch für die globale Warteschlange, aus der Elemente entnommen werden, sobald die Worker-Threads keine Arbeit mehr von anderen Threads stehlen können.

Das soeben beschriebene Konzept hat mehrere Vorteile. Man muss sich vergegenwärtigen, dass die „jüngsten“ Tasks in der Regel die kleinsten sind (auf rekursive Weise), darum die LIFO-(Stack)- Reihenfolge für lokale Tasks. Wenn Arbeit von anderen lokalen Queues gestohlen wird, dann ist es sinnvoll, den „größten“ Task zu schnappen, der wahrscheinlich auch der älteste in jener Queue sein wird, darum die FIFO-(Pipeline)-Reihenfolge. Das Gleiche gilt für die globale Queue (der älteste Task wird wahrscheinlich auch der größte sein).

Der Code in Listing 5 stellt den eigentlichen Berechnungsteil dar. Der Code in Listing 6 zeigt die Hauptklasse, die den Fork-Join-Pool und die Berechnungs-Action initialisiert. Das Zeitstempel-Diagramm in Abbildung 3 zeigt eine weitere signifikante Beschleunigung.

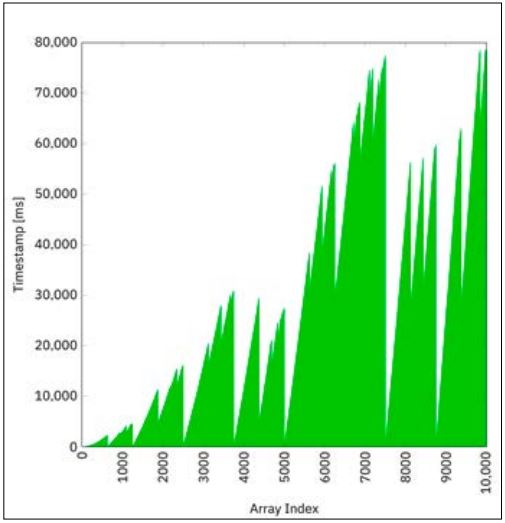
Abb. 3: Fork-Join-Pool mit Invoke-All-Berechnung

import java.time.*;
import java.util.concurrent.*;
public final class ForkJoinPoolInvokeAllComputation {
private static final int ARRAY_SIZE = 10_000;
private TimestampedValue[] array = new TimestampedValue[ARRAY_SIZE];
public static void main(String[] args) throws InterruptedException {
 ForkJoinPoolInvokeAllComputation computation
 = new ForkJoinPoolInvokeAllComputation();
 computation.setUpAndInvokeComputation();
 // computation.printTimestamps();
}
private void setUpAndInvokeComputation() throws InterruptedException {
Instant startTime = Instant.now();
 ForkJoinTask<Void> action
 = new InvokeAllComputationAction(0, ARRAY_SIZE,
 array, startTime);
ForkJoinPool pool = new ForkJoinPool();
 pool.invoke(action);
}
/* [...] Method printTimestamps() omitted. */
}

Listing 6: Initialisierung des Fork-Join-Pools

Die ganze Berechnung ist nun innerhalb von 79 s abgeschlossen, was ungefähr 40 Prozent schneller als die Berechnung in einem Thread-Pool mit fixer Größe aus dem vorhergehenden Abschnitt und mehr als 7-mal schneller als die Berechnung in einem einzelnen Thread ist. Dies ist der Tatsache geschuldet, dass Threads, die keine Arbeit mehr haben – was bei den Kleine-Index-Threads häufiger vorkommen wird als bei den Große-Index-Threads –, aushelfen und Arbeit übernehmen, die ursprünglich anderen Worker-Threads zugewiesen war. Dieses ganze Verhalten erklärt auch das „chaotische“ Muster des Diagramms in Abbildung 3.

Fork-Join-Pool mit Fork-Join-Berechnung

Der vorherige Abschnitt hat das Fork-Join-Framework verwendet, allerdings gab es dabei keine expliziten fork- oder join-Aufrufe. Diese benötigt man, wenn man an den Resultaten der Berechnung eines Subtasks interessiert ist. Im Blog-Eintrag des Autors zu diesem Thema findet der Leser noch ein weiteres Codebeispiel, das einen expliziten Fork-Join-Mechanismus verwendet, um die Summe aller array-Elemente zu berechnen – natürlich rekursiv [Blog].

Fazit

Abbildung 4 zeigt alle vier Szenarios in einem einzigen Diagramm vereint. Die Beschaffenheit der Problemstellung lässt das Fork-Join-Framework am besten performen. Das einfache Aufteilen des Tasks in n Subtasks und diese dann parallel abzuarbeiten, verhält sich aufgrund der ungleichen Berechnungszeiten der Array-Werte nicht so gut. Allerdings ist der Quelltext jenes Thread-Pool-Verfahrens wesentlich kürzer.

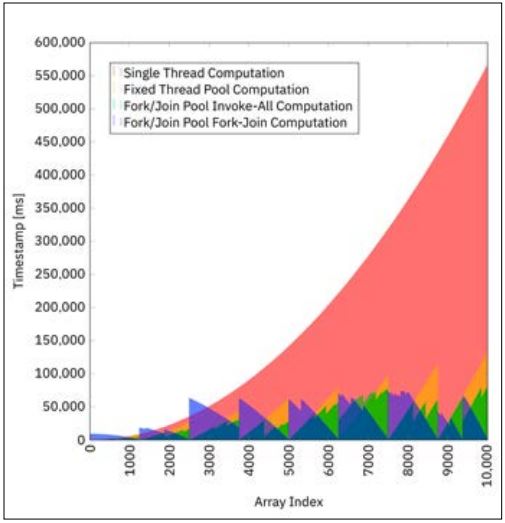
Abb. 4: Vergleich aller vier Berechnungsmethoden

Die Botschaft ist klar: In der nebenläufigen Programmierung gibt es keine Einheitslösung. Man muss zuerst das darunterliegende Problem analysiert haben, ehe man den (hoffentlich einfachsten) Algorithmus anwenden kann. Das Fork-Join-Framework ist sehr flexibel und kann sich selbst „asymmetrischen“ Situationen perfekt anpassen. Allerdings erfolgt dies auf Kosten von mehr Boilerplate-Code. Hoffentlich kann der hier vorliegende Artikel helfen, wenn in Zukunft eine eigene Fork-Join-Berechnung implementiert werden muss.